โดย วีรยุทธ เลิศบำรุงสุข
HIGHLIGHTS
- Active inequality constraints คือข้อจำกัดแบบไม่เท่าเทียมที่ค่าคำตอบเหมาะสุดเกิดขึ้น
- บ่อยครั้งการดำเนินการที่เหมาะสุดจะนำไปสู่การควบคุมระบบไว้ที่ active inequality constraints
สภาวะดำเนินการที่เหมาะสุดและการควบคุมค่าที่ขอบเขตของข้อจำกัด (Optimal operating condition and active constraint control)
บ่อยครั้งการดำเนินการในกระบวนการ มักจะมีทางเลือกของสภาวะดำเนินการ (operating condition) ที่เป็นไปได้หลายทางเลือก การเลือกการดำเนินการที่เหมาะสุดจึงเป็นสิ่งสำคัญในการลดต้นทุนหรือเพิ่มกำไรในการผลิต โดยทั่วไปการดำเนินการที่เหมาะสุดจะเกี่ยวข้องกับการแก้ปัญหาหาค่าเหมาะสุดแบบออนไลน์ (online optimization) โดยความถี่ในการหาค่าเหมาะสุดซ้ำ (reoptimization) นั้นจะขึ้นกับสเกลเวลา (time scale) หรือความถี่(ความรวดเร็ว)ของการเปลี่ยนแปลงของสิ่งรบกวนของกระบวนการ อย่างไรก็ตาม ในบางปัญหาที่มีความเป็นเชิงเส้น (linear) หรือความไม่เชิงเส้นน้อย (mildly nonlinear) จะพบว่าการดำเนินการที่เหมาะสุดมักจะเกิดขึ้นที่ขอบเขตของเฉพาะบางข้อจำกัดแบบไม่เท่าเทียม (active inequality constraints) ซึ่งหมายความว่าหากสามารถควบคุมระบบให้อยู่ที่ขอบเขตของข้อจำกัดแบบไม่เท่าเทียมดังกล่าว (active inequality constraints) ได้ ก็จะได้สภาวะการดำเนินการที่เหมาะสุดนั่นเอง อนึ่ง ในโลกความเป็นจริงระบบจะต้องอยู่บนข้อจำกัดแบบเท่าเทียม (active equality constraints) อยู่เสมอ
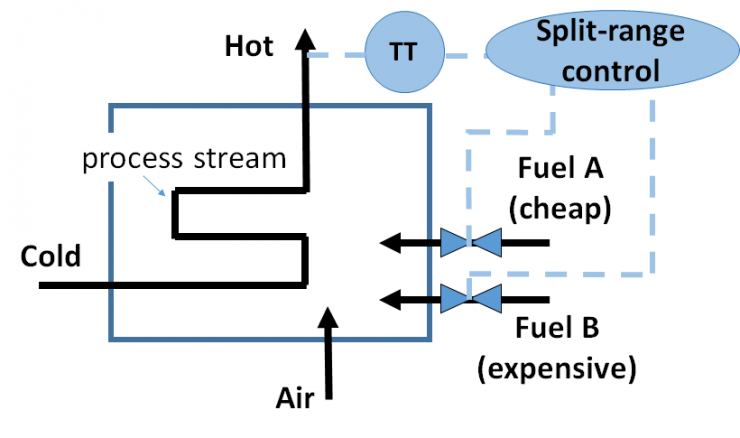
เพื่อให้เห็นภาพมากขึ้น ลองมาดูตัวอย่างเตาเผาดังรูปที่ 1 ซึ่งมีการติดตั้งหัวเผา 2 หัวที่ใช้แหล่งเชื้อเพลิง 2 ชนิด คือ ชนิด A ที่มีราคาถูก และชนิด B ที่มีราคาแพง จะเห็นว่าปัญหาการดำเนินการของเตาเผาจะมีได้หลายทางเลือก ตามสัดส่วนว่าจะเลือกใช้เชื้อเพลิงชนิด A และ B ในปริมาณเท่าไร

การแก้ปัญหาสภาวะดำเนินการเหมาะที่สุดดังกล่าว จะเกี่ยวข้องกับการหาค่าอัตราการไหลของเชื้อเพลิง A และ B (FA, FB) เพื่อให้มีต้นทุนดำเนินการต่ำที่สุด ซึ่งสามารถเขียนได้เป็นปัญหาการหาค่าเหมาะสุดอย่างง่าย ดังนี้
min cost = [cost of fuel A] + [cost of fuel B]
s.t. Tfurnace = Ttarget …..h1
FA,min <= FA <= FA,max …..g1
FB,min <= FB <= FB,max …..g2
จากการวิเคราะห์ปัญหาจะพบว่าองศาอิสระ (degrees of freedom) ของปัญหามีค่าเท่ากับ 1 (degrees of freedom = number of variables – number of equality constraints = 2 – 1 = 1 เมื่อตัวแปรคือ FA&FB และข้อจำกัดแบบเท่าเทียมคือ h1) การที่องศาอิสระมีค่ามากกว่าศูนย์ หมายความว่าปัญหาการดำเนินการดังกล่าวมีคำตอบที่เป็นไปได้หลายคำตอบ จึงจำเป็นต้องหาทางเลือกการดำเนินการที่เหมาะสุด ซึ่งจะพบว่าเกิดได้ 2 กรณีคือ
กรณีที่ 1 ใช้เชื้อเพลิง A อย่างเดียว (ที่ equality constraint h1 และ active inequality constraint เกิดที่ขีดจำกัดล่างของ g2 ซึ่งเป็นศูนย์)
ในกรณีที่ความต้องการอุณหภูมิขาออกของสาย process stream มีค่าไม่สูงมาก จะพบว่าเพื่อให้ได้ต้นทุนดำเนินการต่ำสุด ควรจะใช้เชื้อเพลิง A ราคาถูกเพียงชนิดเดียว ซึ่งหมายถึงการปรับวาล์วสายป้อนเชื้อเพลิง A จนได้ค่าอุณหภูมิตามต้องการ (ตาม equality constraint h1) และปิดวาล์วสายป้อนเชื้อเพลิง B (active inequality constraint เกิดที่ขอบเขตของขีดจำกัดล่าง(เท่ากับศูนย์)ของสายเชื้อเพลิง B, g2 โดย FB = FB,min = 0)
กรณีที่ 2 ใช้ทั้งเชื้อเพลิง A และ B (ที่ equality constraint h1 และ active inequality constraint เกิดที่ขีดจำกัดบนของ g1)
ในกรณีที่ความต้องการอุณหภูมิขาออกของสาย process stream สูงเกินกว่าค่าๆ หนึ่ง จะพบว่าการใช้เพียงเชื้อเพลิง A เพียงชนิดเดียวจะมีปริมาณไม่เพียงพอ จึงจำเป็นต้องใช้เชื้อเพลิงชนิด B ที่มีราคาสูงมาเสริมด้วย ซึ่งหมายถึงวาล์วของสายป้อนเชื้อเพลิง A ต้องเปิดจนสุด (active inequality constraint เกิดที่ขอบของขีดจำกัดบนของสายเชื้อเพลิง A, g1 โดย FA=FA,max) และทำการปรับวาล์วสายป้อนเชื้อเพลิง B ช่วยเพื่อให้ได้ค่าอุณหภูมิตามต้องการ (equality constraint h1)
จากปัญหาข้างต้นจะพบว่าในกรณีของกระบวนการที่ไม่ซับซ้อนดังปัญหาเตาเผาที่ติดตั้งหัวเผา 2 หัว ปัญหาการดำเนินการที่เหมาะสุดอาจไม่จำเป็นต้องแก้ปัญหาการหาค่าเหมาะสุดแบบออนไลน์ (online optimization) ทั้งนี้หากสามารถหา control policy ที่สามารถควบคุมกระบวนการให้อยู่ที่ขอบเขตของ active inequality constraint ที่เหมาะสมได้ (ซึ่งในที่นี้ก็คือการคุมปริมาณการใช้เชื้อเพลิง A และ B) ระบบก็จะอยู่ที่สภาวะดำเนินการที่เหมาะสุดได้เอง โดยตัวอย่างของ control policy ที่ผ่านการใช้ split-range control ของระบบเตาเผาจะแสดงได้ดังรูปที่ 2


ABOUT THE AUTHOR
วีรยุทธ เลิศบำรุงสุข
ภาควิชาวิศวกรรมเคมี คณะวิศวกรรมศาสตร์ฯ
มหาวิทยาลัยศิลปากร