Well-Mixed System? Lumped or Distributed Parameter Systems

07/03/2022 by Macross
Publications

โดย วีรยุทธ เลิศบำรุงสุข

HIGHLIGHTS

ระบบที่มีการผสมกันอย่างสมบูรณ์เรียกได้เป็นระบบพารามิเตอร์แบบก้อน
ระบบพารามิเตอร์แบบกระจายจะมีค่าของตัวแปรที่ขึ้นกับตำแหน่ง

บทความที่แล้วได้พูดถึงความหมายของสถานะคงตัวและสถานะไม่คงตัว ซึ่งกำหนดจากสมมติฐานว่าระบบอยู่ที่สถานะคงตัวหรือไม่ หรือสิ่งที่สนใจเปลี่ยนแปลงตามเวลาหรือไม่ ในบทความนี้เราจะมาทบทวนความหมายของอีกหนึ่งสมมติฐานที่นิยมใช้กัน นั่นคือสมมติฐานที่กำหนดให้ระบบมีการผสมกันอย่างสมบูรณ์ (well-mixed system) ซึ่งส่งผลว่าสิ่งที่สนใจจะขึ้นอยู่กับตำแหน่งหรือไม่ หรืออีกนัยหนึ่งคือเป็นระบบพารามิเตอร์แบบก้อน (lumped parameter system) หรือระบบพารามิเตอร์แบบกระจาย (distributed parameter system)

ระบบพารามิเตอร์แบบก้อน (Lumped parameter system)

ในทางวิศวกรรมเคมี การผสมสารนับเป็นปฏิบัติการสำคัญเพื่อให้สารในระบบมีความเป็นเนื้อเดียวกัน หรือในอีกนัยหนึ่งก็คือมีคุณสมบัติเดียวกันทั้งระบบ เพื่อให้เห็นภาพ ลองพิจารณาระบบถังผสมดังรูปที่ 1 ที่ประกอบด้วยสายป้อนสายที่ 1 ที่มีค่าอุณหภูมิ T1 และสายป้อนสายที่ 2 ที่มีค่าอุณหภูมิ T2

เนื่องจากถังผสมมีการติดตั้งใบกวน และถ้ามีการออกแบบได้ดีพอ จะสามารถสมมติได้ว่าเมื่อสายป้อนที่ 1 และ 2 เข้าสู่ถังกวน จะถูกผสมรวมกับสารในถังผสมทันทีเป็นเนื้อเดียวกัน ส่งผลให้สารภายในถังตลอดจนที่ตำแหน่งขาออกมีค่าอุณหภูมิ T เหมือนกันทั้งถัง หรือถ้ากล่าวให้ชัดขึ้นก็คือ ค่าอุณหภูมิของสารจะไม่ขึ้นกับตำแหน่งในระบบ และค่าอุณหภูมิ T ค่าเดียวสามารถเป็นตัวแทนของทั้งระบบได้ กรณีนี้จะเรียกเป็นระบบพารามิเตอร์แบบก้อน (lumped parameter system)

จากระบบถังผสมในรูปที่ 1 หากสนใจระบบที่สถานะคงตัว (ไม่ขึ้นกับเวลา) จะเขียนสมการดุลพลังงานรอบถังผสมได้ดังนี้

เมื่อ

m1, m2 คือ อัตราการไหลเชิงมวลของสายป้อนที่ 1 และ 2
T1, T2, T คือ ค่าอุณหภูมิของสายป้อนที่ 1, สายป้อนที่ 2, และสายขาออก
Cp คือ ค่าความจุความร้อนจําเพาะเชิงมวลของสาร

ในการแก้สมการที่ 1 เพื่อหาค่าอุณหภูมิ T จะพบว่าเกี่ยวข้องกับการแก้สมการพีชคณิต (algebraic equation) และได้คำตอบคือ

ระบบพารามิเตอร์แบบกระจาย (Distributed parameter system)

ในระบบหนึ่งๆ หากสามารถกำหนดสมมติฐาน “ระบบมีการผสมกันอย่างสมบูรณ์” จะหมายความว่าค่าเดียวของตัวแปรสามารถเป็นตัวแทนของทั้งระบบได้ อย่างไรก็ตาม หากสมมติฐานดังกล่าวไม่เป็นจริง จะหมายถึงว่าค่าของตัวแปรที่แต่ละตำแหน่งในระบบจะมีค่าไม่เท่ากัน เช่น กรณีของระบบถังผสมที่มีการกวนผสมไม่สมบูรณ์ หากมองถังผสมเป็น 3 มิติ และใช้พิกัดคาร์ทีเซียน (Cartesian coordinate system) ในการกำหนดตำแหน่ง จะพบว่าค่าอุณหภูมิ T = T(x, y, z) จะขึ้นอยู่กับตำแหน่ง x, y และ z ภายในถัง ซึ่งไม่จำเป็นต้องมีค่าเท่ากันในทุกตำแหน่ง กรณีนี้จะเรียกเป็นระบบพารามิเตอร์แบบกระจาย (distributed parameter system)

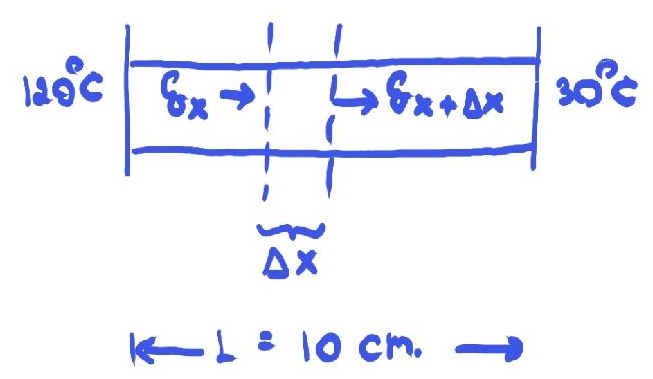
เพื่อให้เห็นภาพของระบบพารามิเตอร์แบบกระจายชัดเจนขึ้น ลองพิจารณาระบบแท่งโลหะนำความร้อนที่ถูกยึดติดกับผนังสองด้านที่มีค่าอุณหภูมิคงที่ต่างกัน ดังรูปที่ 2

ในกรณีที่สนใจค่าอุณหภูมิที่ตำแหน่งต่างๆ ของแท่งโลหะ จะพบว่าหากพิจารณาที่ตำแหน่งใกล้ผนังฝั่งซ้าย ค่าอุณหภูมิจะมีค่าใกล้กับ 120 องศาเซลเซียส แต่หากพิจารณาที่ตำแหน่งใกล้ฝั่งขวา ค่าอุณหภูมิจะมีค่าใกล้กับ 30 องศาเซลเซียส สังเกตว่าในระบบดังกล่าว ค่าอุณหภูมิเพียงค่าเดียวไม่สามารถเป็นตัวแทนของทั้งแท่งโลหะได้ เนื่องจากสมมติฐานที่ว่า “ระบบมีการผสมกันอย่างสมบูรณ์” ไม่เป็นจริง หรือก็คือ อุณหภูมิมีค่าแปรผันตามตำแหน่ง เช่น ถ้าสนใจการเปลี่ยนแปลงของอุณหภูมิในทิศ x เพียงทิศเดียว (ซึ่งสมเหตุสมผลเมื่อแท่งโลหะมีความเรียวยาว) จะได้ว่า T = T(x)

จากระบบแท่งโลหะนำความร้อนในรูปที่ 2 เนื่องจากค่าอุณหภูมิไม่คงที่เท่ากันทั้งแท่ง ดังนั้นขอบเขตของการเขียนสมการดุลพลังงานจะไม่สามารถพิจารณาทั้งก้อนได้ แต่จะต้องทำการเขียนสมการดุลพลังงานที่ส่วนย่อยเล็กๆ ของแท่งโลหะแทน กรณีที่สนใจระบบที่สถานะคงตัว จะสามารถเขียนได้ดังนี้