Blog

โดย วีรยุทธ เลิศบำรุงสุข

---

HIGHLIGHTS

• Near optimal operation คือการดำเนินการที่สภาวะใกล้เคียงกับสภาวะดำเนินการที่เหมาะสุด ซึ่งสามารถทดแทนออนไลน์ออพติไมเซชัน (online optimization) ได้
• ในบางกระบวนการ เราสามารถเปลี่ยนปัญหา online optimization ให้เป็นปัญหา feedback control ที่สภาวะใกล้เคียงกับการดำเนินการที่เหมาะสุด

---

ในกรณีที่สภาวะการดำเนินการที่เหมาะสุดเกิดที่ตำแหน่งขอบเขตของข้อจำกัดไม่เท่าเทียม (active inequality constraints) ดังตัวอย่างเตาเผาในตอนที่แล้ว ความท้าทายของการดำเนินการที่เหมาะสุดจะเป็นการควบคุมระบบให้อยู่ที่ขอบเขตของข้อจำกัดไม่เท่าเทียม (active inequality constraints) ที่เกี่ยวข้อง

หากสภาวะดำเนินการที่ให้ค่าต่ำสุดเกิดที่ตำแหน่งหลุม(จุดต่ำสุด)ของฟังก์ชันวัตถุประสงค์ การดำเนินการที่ต่ำสุดจะเป็นการควบคุมระบบให้อยู่ที่จุดหลุมนั้น โชคไม่ดีที่การเปลี่ยนแปลงของสิ่งรบกวนระบบ อาจส่งผลให้สภาวะดำเนินการที่ต่ำสุดขยับเปลี่ยนไป จึงจำเป็นต้องทำการแก้ปัญหาหาค่าที่เหมาะสุดซ้ำ (reoptimization) ซึ่งเกี่ยวข้องกับการทำ online optimization ในกรณีของกระบวนการผลิตแบบต่อเนื่อง

อย่างไรก็ตามในบางปัญหา หากเลือกตัวแปรควบคุม (controlled variable) และตั้งค่าเป้าหมาย (set point) ได้ถูกต้อง การควบคุมระบบให้อยู่ใกล้สภาะวะดำเนินการที่เหมาะสุดเดิมนั้นจะมิได้ส่งผลให้ค่าฟังก์ชัน วัตถุประสงค์เปลี่ยนแปลงไปอย่างมีนัยสำคัญ นั่นคือยังอยู่ในสภาวะ near optimal operation ในระดับที่ยอมรับได้ จึงสามารถหลีกเลี่ยงหรือทดแทนการทำ online optimization ได้

สภาวะดำเนินการ Near Optimal Operation

พิจารณาปัญหา unconstrained optimization P1 ที่ได้จากการลดจำนวนตัวแปรอิสระโดยการอาศัย equality constraints และ active inequality constraints ดังต่อไปนี้

เมื่อ u คือตัวแปรอิสระ (degrees of freedom) หรือตัวแปรปรับกระบวนการ (manipulated variable) ที่เหลือหลังจากการใช้ตอบสนอง equality constraints และ active inequality constraints แล้ว

d คือตัวแปรที่ส่งผลรบกวน

จากการแก้ปัญหา P1 ค่า u_opt (ค่า u ที่ทำให้ J มีค่าต่ำที่สุด) จะสามารถเปลี่ยนแปลงตามการเปลี่ยนค่าของ d นั่นคือ เมื่อค่า d ขยับเปลี่ยน จะต้องมีการทำ reoptimization เพื่อหาค่า J_opt และ u_opt ใหม่ทุกครั้ง

อย่างไรก็ตาม เพื่อลดความยุ่งยากของการทำ reoptimization ด้วย online optimization ได้มีผู้เชี่ยวชาญ (เช่น Skogestad, 2000) เสนอแนวคิดหาวิธีการควบคุมระบบให้อยู่ที่สภาวะ near optimal operation ภายใต้การเปลี่ยนแปลงของตัวแปรรบกวน d ดังเช่นแนวคิดในรูปที่ 1

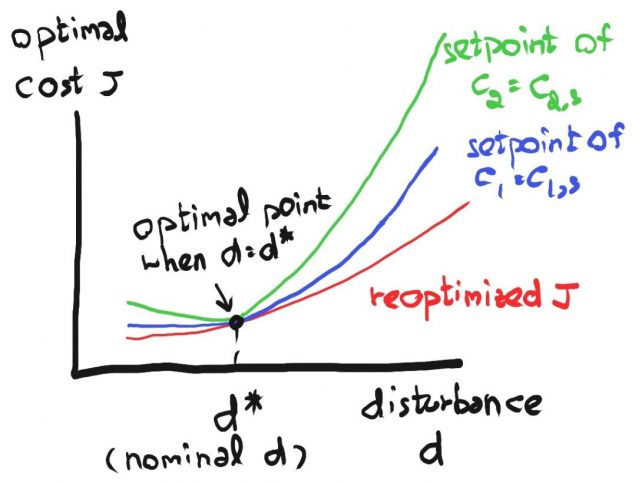
รูปที่ 1 สามารถอธิบายได้ดังนี้

• สมมติว่า เมื่อทำการแก้ปัญหา P1 โดยใช้ค่า nominal ของ d (d*) พบว่าได้ค่า Cost J ต่ำสุดที่ u_opt ค่าหนึ่ง ซึ่งเปรียบเสมือนค่าตัวแปรดำเนินการของระบบที่ c₁=c_1,s และ c₂=c_2,s
• เมื่อตัวแปร d เกิดเปลี่ยนค่าไป หากทำการ reoptimize ปัญหา P1 จะได้ผลใหม่เป็นดังเส้นสีแดงในรูปที่ 1 (ซึ่งสอดคล้องกับค่า J_opt และ u_opt ที่เปลี่ยนไปตาม d นั่นคือ J_opt(d) และ u_opt(d))
• หากลดภาระการทำ reoptimization โดยเพียงควบคุม c₁ให้อยู่ที่ set point c_1,s หรือ c₂ให้อยู่ที่ set point c_2,s โดยผ่านการปรับค่า u ด้วย feedback control จะได้ผลดังเส้นสีฟ้าและเส้นสีเขียวตามลำดับ

จากรูปจะเห็นว่าการควบคุม c₁ ของระบบโดยตั้ง set point c₁=c_1,s จะมีค่า cost J ต่างจากเส้นสีแดงน้อยกว่ากรณีเส้นสีเขียว ดังนั้นหากผลต่างนี้อยู่ในระดับที่ยอมรับได้ จะหมายความว่าเราสามารถเปลี่ยนปัญหา reoptimization ให้เป็นปัญหา feedback control โดยประมาณได้  นั่นคือ จะคำนวณหาค่า u_opt โดยคร่าวๆ ผ่าน feedback control law โดยควบคุมค่า c₁ ให้อยู่ที่ set point c_1,s แทนการแก้ปัญหา online optimization นั่นเอง

Optimal blending of gasoline

เพื่อให้เห็นภาพชัดเจนขึ้น ลองพิจารณาตัวอย่างปัญหาการผสมแก๊สโซลีน โดยกำหนดปัญหา P2 คือ ต้องการผลิตแก๊สโซลีนอย่างต่อเนื่องในอัตรา 1 kg/s โดยมีค่าออกเทนไม่น้อยกว่า 98 และมีต้นทุนต่ำสุดจากการผสมสายการไหล 3 สาย (ในปริมาณ m₁, m₂, และ m₃ kg/s ตามลำดับ) ได้แก่

• สายการไหลที่ 1 มีค่าออกเทน 99 และมีต้นทุนแปรผันตามปริมาณดังสมการ p₁ = 0.1(1+m₁) $/kg
• สายการไหลที่ 2 มีค่าออกเทน 105 และมีต้นทุนคือ p₂ = 0.2 $/kg
• สายการไหลที่ 3 มีค่าออกเทน d¹ และมีต้นทุนคือ p₃ = 0.12 $/kg

¹สายการไหลที่ 3 มีค่าออกเทน nominal ที่ d* = 95 โดยมีค่าผันผวนในช่วง 95-97

อนึ่ง ค่าออกเทนของสายผสมคำนวณได้จากการเฉลี่ยค่าออกเทนด้วยปริมาณของแต่ละสาย

จากข้อมูลที่กำหนดสามารถสร้างปัญหา P2 เป็นปัญหาการหาค่าต่ำที่สุดได้ดังนี้

จากปัญหา P2 พบว่ามีตัวแปรดำเนินการจำนวน 3 ตัวแปร (m₁, m₂, m₃) และ equality constraint 1 เงื่อนไข (h₁) ดังนั้นค่า degrees of freedom จะเหลือเท่ากับ 2 (degrees of freedom = number of variables – number of equality constraints = 3 – 1 = 2) นั่นคือ ตัวแปรดำเนินการ 1 ตัวจะถูกใช้เพื่อ ตอบสนอง equality constraint h₁ (เพื่อให้ได้กำลังการผลิตแก๊สโซลีน 1 kg/s)

เมื่อลองทำการหาค่า J ต่ำสุดของปัญหา P2 ภายใต้การเปลี่ยนแปลงค่าออกเทนของสายการไหลที่ 3 ในช่วง 95-97 พบว่า inequality constraint g₁ จะ active เสมอ ซึ่งหมายความว่า ตัวแปรดำเนินการอีก 1 ตัวต้องถูกใช้เพื่อตอบสนอง active inequality constraint g₁ เสมอ (เพื่อให้ได้ค่าออกเทนผสมที่ 98)

การวิเคราะห์ข้างต้นบอกให้ทราบว่ายังคงเหลือตัวแปรดำเนินการเพียง 1 ตัวที่เป็นตัวแปรอิสระ ดังนั้นหากต้องการหลีกเลี่ยงการทำ online optimization ก็สามารถพิจารณาใช้ตัวแปรดำเนินการที่เหลือนี้ในการควบคุมต้นทุน J (โดยการควบคุมตัวแปรดำเนินการ c ที่เลือกอย่างเหมาะสมเพื่อให้ระบบอยู่ที่สภาวะ near optimal operation) โดยการใช้ feedback control และอ้างอิงตารางที่ 1

ตารางที่ 1 ผลการเปรียบเทียบค่า Cost J ที่เกิดจากการทำ Reoptimization (online optimization) กับค่าของกรณีการควบคุมระบบให้อยู่ที่สภาวะ near optimal operation ภายใต้การขยับเปลี่ยนของตัวแปรรบกวน d (ค่าออกเทนของสายการไหลที่ 3)

อนึ่ง ข้อมูลเพิ่มเติมเกี่ยวกับการเลือกตัวแปรดำเนินการ c เพื่อควบคุมนั้นสามารถศึกษาได้จากงานของ Skogestad (2000, 2004)

สรุปแล้ว เมื่อทำการแก้ปัญหา P2 ที่สภาวะ Nominal (ค่าออกเทนของสายการไหลที่ 3 = 95) จะได้คำตอบต้นทุนต่ำสุดคือ J = 0.1372 ที่ค่าตัวแปร m₁ = 0.2600, m₂ = 0.1960, และ m₃ = 0.5440  ดังนั้น ค่าของ m₁, m₂ หรือ m₃ ดังกล่าวจึงอาจถูกใช้เป็นค่าเป้าหมาย (set point) สำหรับการควบคุมระบบให้อยู่ที่สภาวะ near optimal operation ต่อไป

ตารางที่ 1 ชี้ให้เห็นว่า ถ้าควบคุมระบบให้อยู่ที่สภาวะ near optimal operation โดยการควบคุมตัวแปรอิสระ m₁ ไว้ที่ set point c_1,s = 0.26 จะเกิดผลต่างน้อยที่สุดจากค่าต่ำสุด cost J ของกรณี online optimization  หากค่าผลต่างดังกล่าวสามารถยอมรับได้ ก็สามารถใช้ feedback control ของตัวแปร m₁ เพื่อทำ near optimal operation แทน online optimization ได้  ตัวอย่างหนึ่งของโครงสร้างระบบควบคุมมีแสดงดังรูปที่ 2

หมายเหตุ ตัวอย่างโครงสร้างระบบควบคุมที่นำเสนอในที่นี้ มีการพิจารณาเพียงในแง่มุมเชิงเศรษฐศาสตร์ ยังมิได้พิจารณาในเชิงความเป็นไปได้ของการควบคุม (controllability) ซึ่งเป็นอีกประเด็นสำคัญที่จะต้องพิจารณาควบคู่ไปด้วย

เนื้อหาบางส่วนในบทความนี้เรียบเรียงและดัดแปลงจากเอกสารอ้างอิงดังนี้

1. Skogestad, S. (2000) Plantwide control: the search for the self-optimizing control structure, Journal of Process Control, 10, 487-507.
2. Skogestad, S. (2004) Near-optimal operation by self-optimizing control: from process control to marathon running and business systems, Computers and Chemical Engineering, 29, 127-137.

---

ABOUT THE AUTHOR

วีรยุทธ เลิศบำรุงสุข

ภาควิชาวิศวกรรมเคมี คณะวิศวกรรมศาสตร์ฯ
มหาวิทยาลัยศิลปากร